I decided to make my own physics rather than rely on Unity’s physics engine. This gives me greater control over how the game feels.

Acceleration/Deceleration Curves

I started with the acceleration curve⁠—how quickly does the plane accelerate from a near-stall to max speed? I recorded footage and reviewed it frame by frame to create a spreadsheet with speed in one column and time in the other. I then tried various regression techniques (linear, quadratic, and logarithmic) to find an equation that would fit the game’s acceleration curve. I specifically chose quadratic and logarithmic equations because I knew I would be able to solve such equations for x (time) given a specific y (speed), which will be important later.

Here is a graph of the full throttle acceleration curve in AC3 starting from the slowest speed I could maintain without stalling. Regression lines are included as well. Minor technical detail: I removed the first 30 frames of observation, where the curve is relatively flat because the throttle hasn’t yet kicked in.

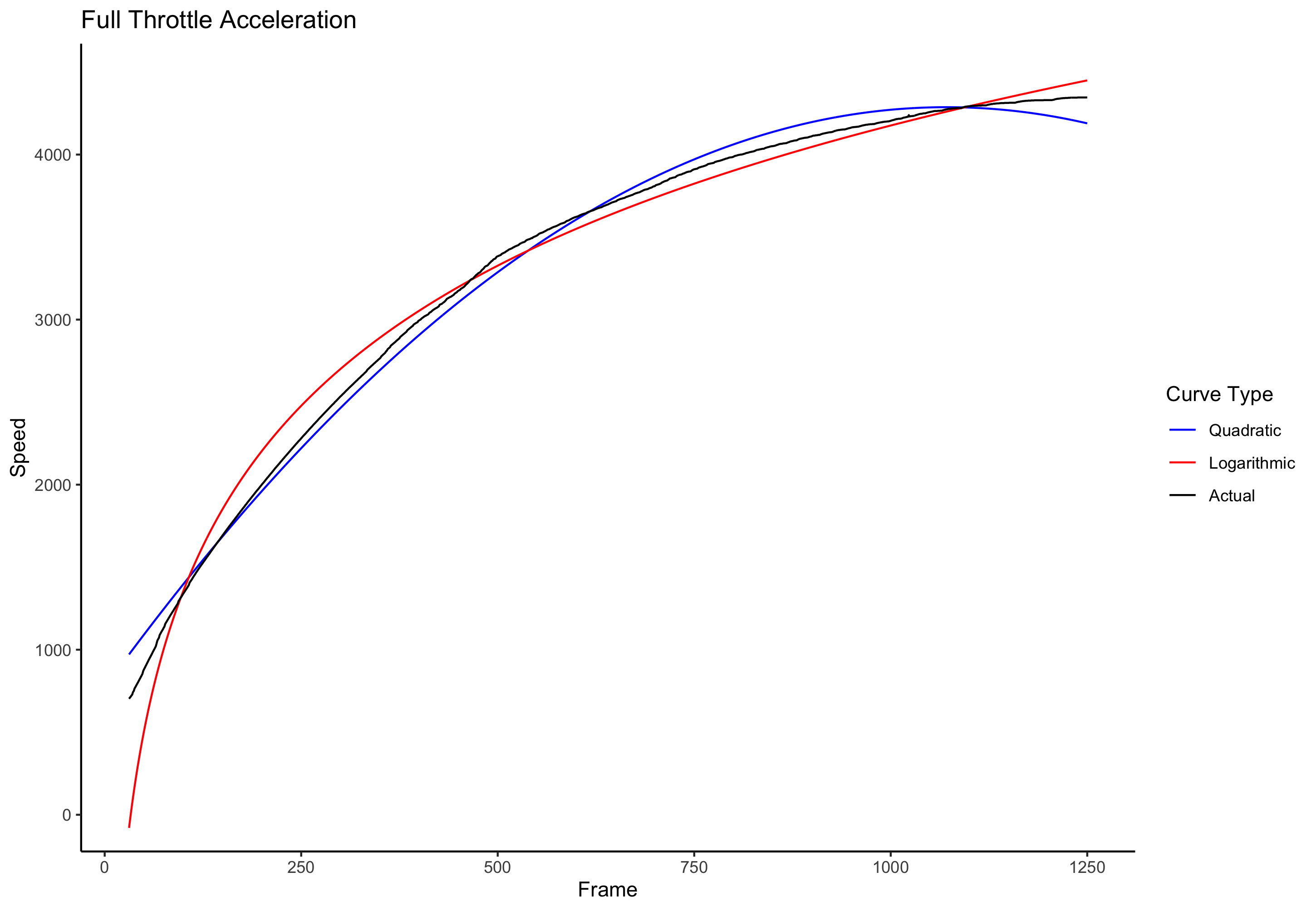
Both regression lines fit pretty well, though the quadratic curve’s inflection point at around frame 1000 is troubling. I will talk about the implications of this later. Removing the last few rows (i.e. the rightmost part of the graph) would shift that inflection point to the right, which might be more sensible.

Here is a similar graph showing speed over time when braking from full speed, with the first 45 frames cut off:

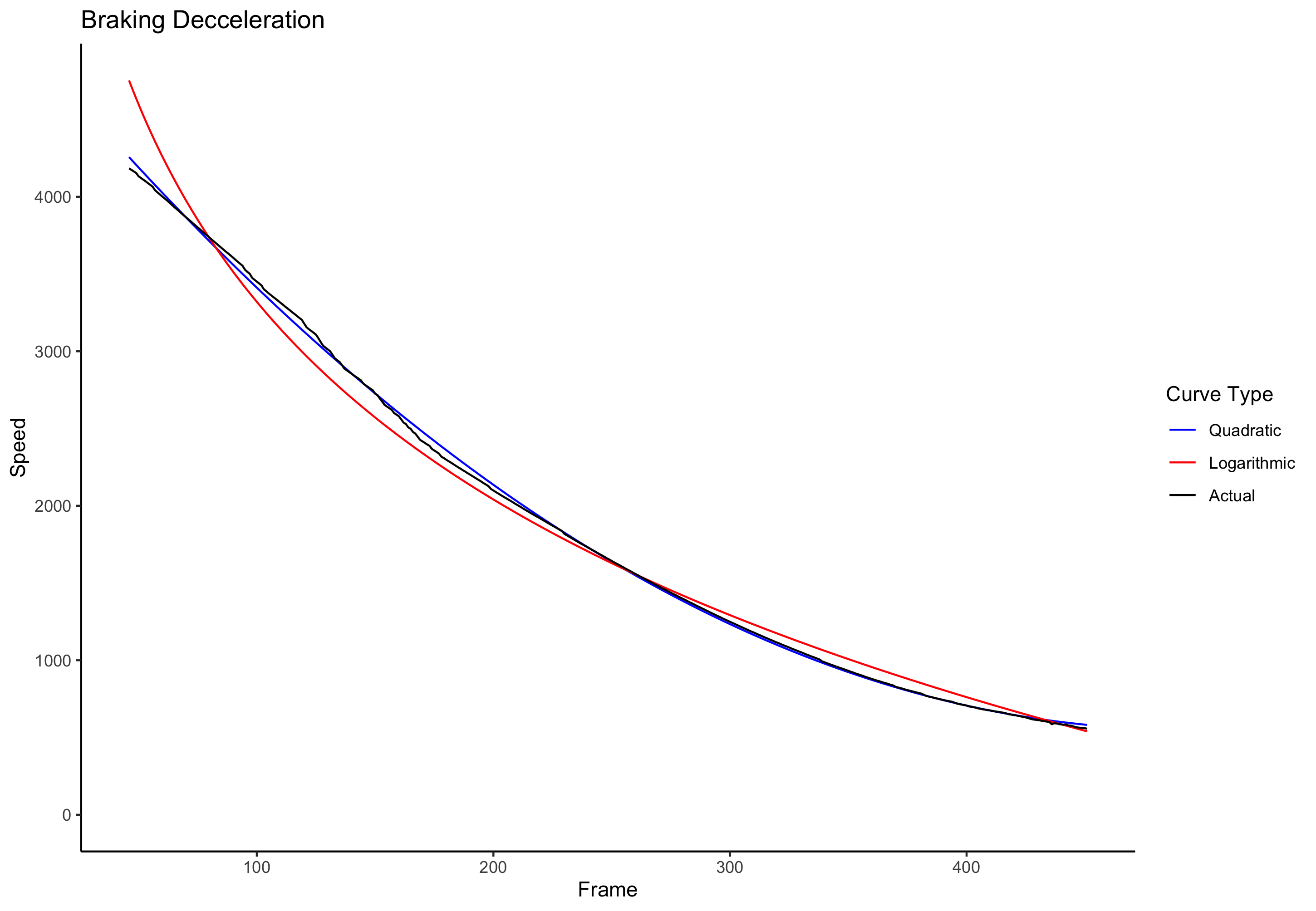
The quadratic curve seems the clear winner here.

Another graph showing the rate of deceleration from full speed with idle throttle (first 10 frames removed):

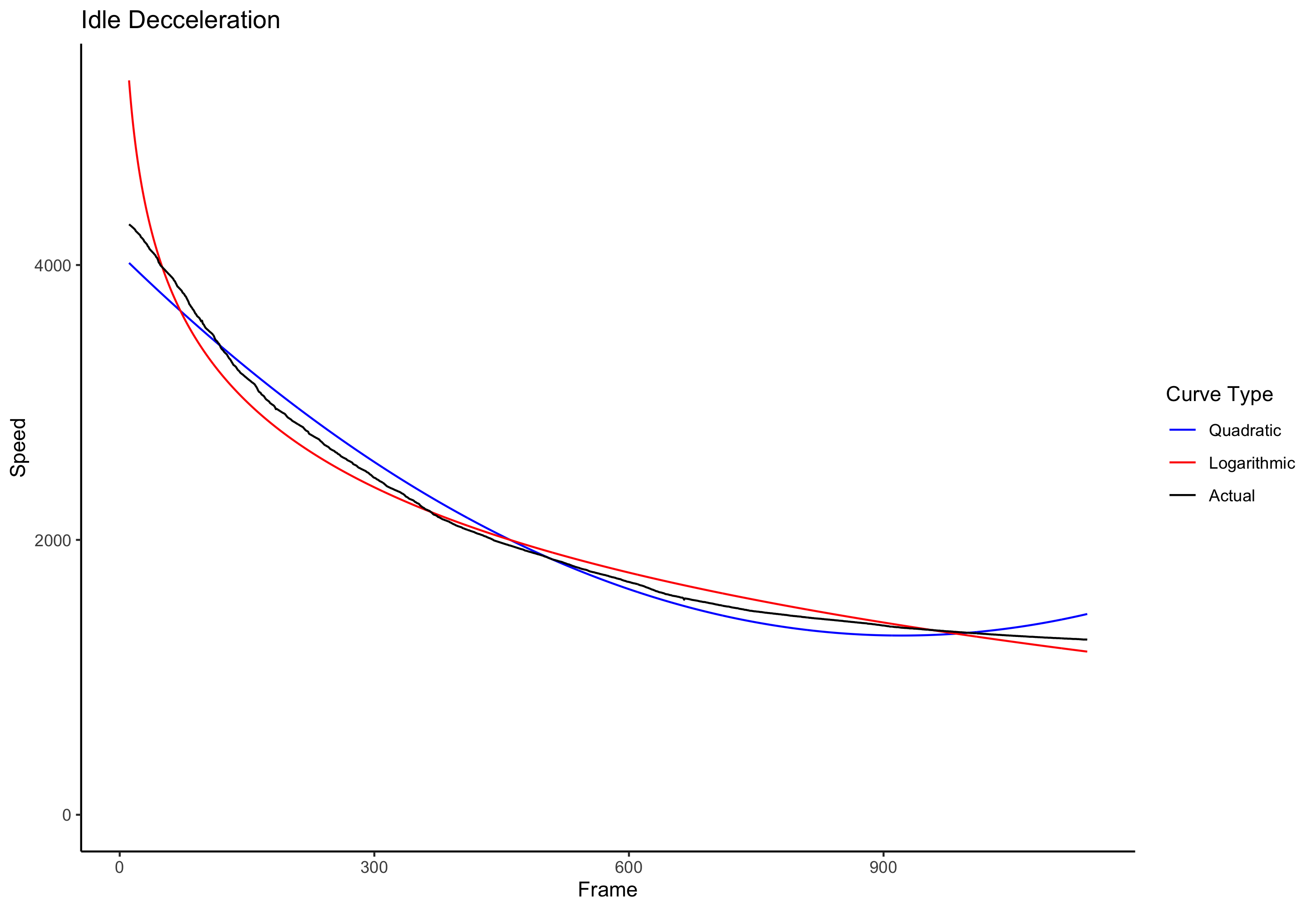
It seems close, but I favor the quadratic curve again. Plus, it’s trickier to solve, and I want to feel like my efforts in testing it were justified :P

Finally, we have acceleration from a near-stall with idle throttle:

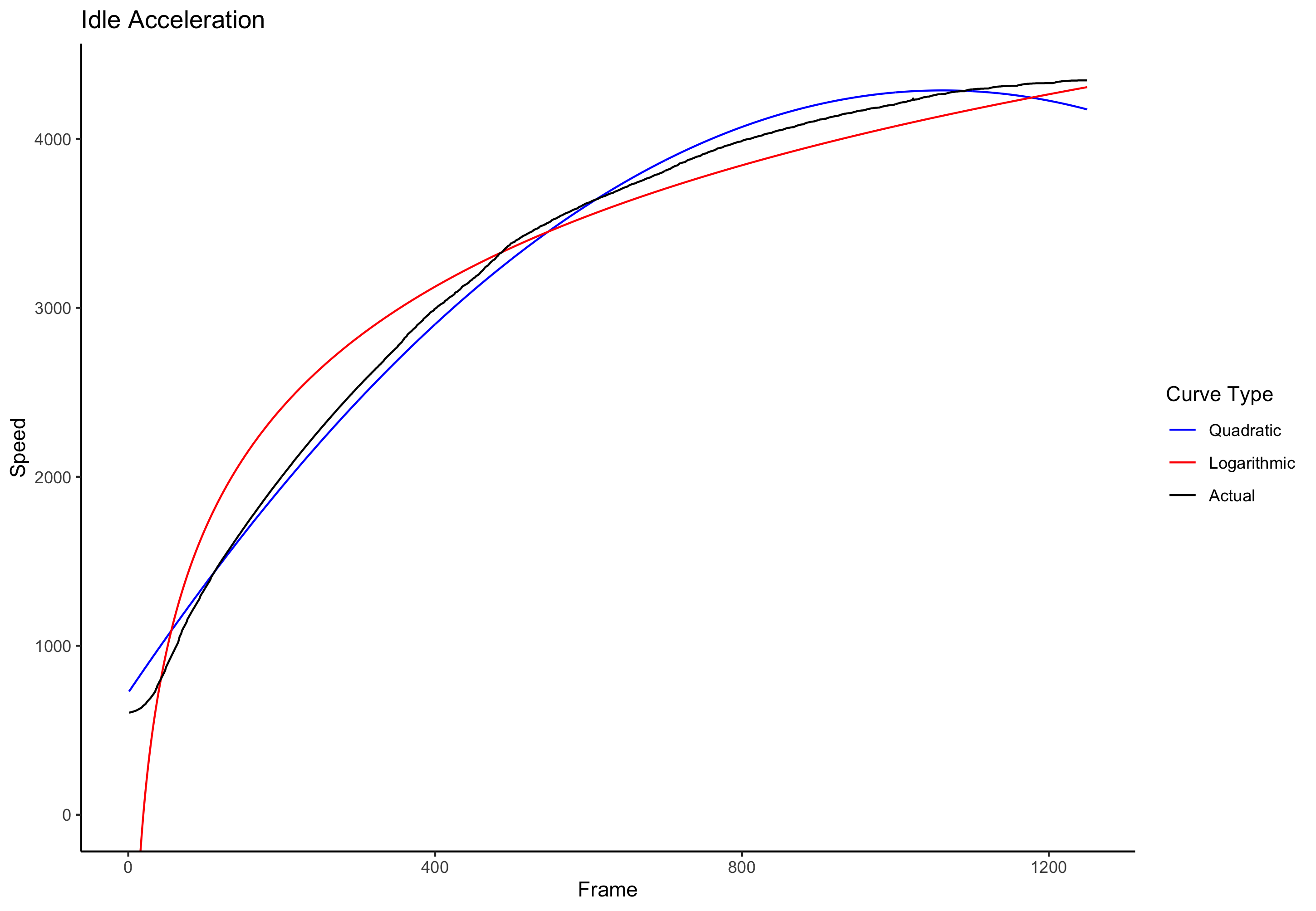
The log curve is too steep at high speed, whereas the quadratic curve seems more or less to get it right.

Overall, I prefer the quadratic curves. In general, I would expect a quadratic equation to fit better than a logarithmic one, since there are two coefficients to tweak rather than just one. Indeed, performing polynomial regression with 5 or so terms produces a more or less perfect fit with every curve, but for practical reasons I opted against using such complex equations.

I followed a pretty simple process to implement these curves into a flight model.

    - First, determine the relevant curve⁠—if the player is accelerating, that would be the acceleration curve, if they are braking, it would be the braking curve, etc.

    - Given the player’s speed and the relevant coefficients and intercepts, solve for x.

    - Increment x to move forward in time[1], then solve for y with that new x. This gives us our new speed assuming the player applied full throttle. But, as in AC3, I programmed the game to take a second or two to transition from idle to full throttle, so instead of assigning the player this new speed, I find the difference between the new and old speed, scale it based on the amount of throttle applied, then add it to the old speed.
        - Things get a bit trickier with quadratic curves because there are two possible x values for any given y. I need to make sure I am solving for the correct side⁠—the left side when the player is decelerating, and the right side when they are accelerating. Further complicating matters is the fact that quadratic curves have a finite domain; it’s impossible to solve for x when the y value greater than the maximum (in the case of n-shaped curves) or smaller than the minimum (in the case of u-shaped curves). In my case, the maximum and minimum values would be difficult but possible to exceed/subceed. As a safeguard, if this happens, I have my code return the player’s speed unaltered.

[1] You might think I would simply increment x by one for each frame, but there’s some conversion involved. I increment by 0.6, because this is happening in Unity’s FixedUpdate loop, which runs about 50 times per second. AC3 runs at 30 fps, so 30fps/50 updates per second gives us a conversion factor of 0.6.

This still leaves us with a few things to account for. For example, air friction⁠—when turning, the player loses speed. To implement this using my previous methodology, I would need to have calculated curves for turning speed while idling, while accelerating, and while decelerating, which seemed unnecessarily laborious. Instead, I measured the effect of air friction by starting a turn from full speed and calculating the deceleration on every frame. The curve looks like this:

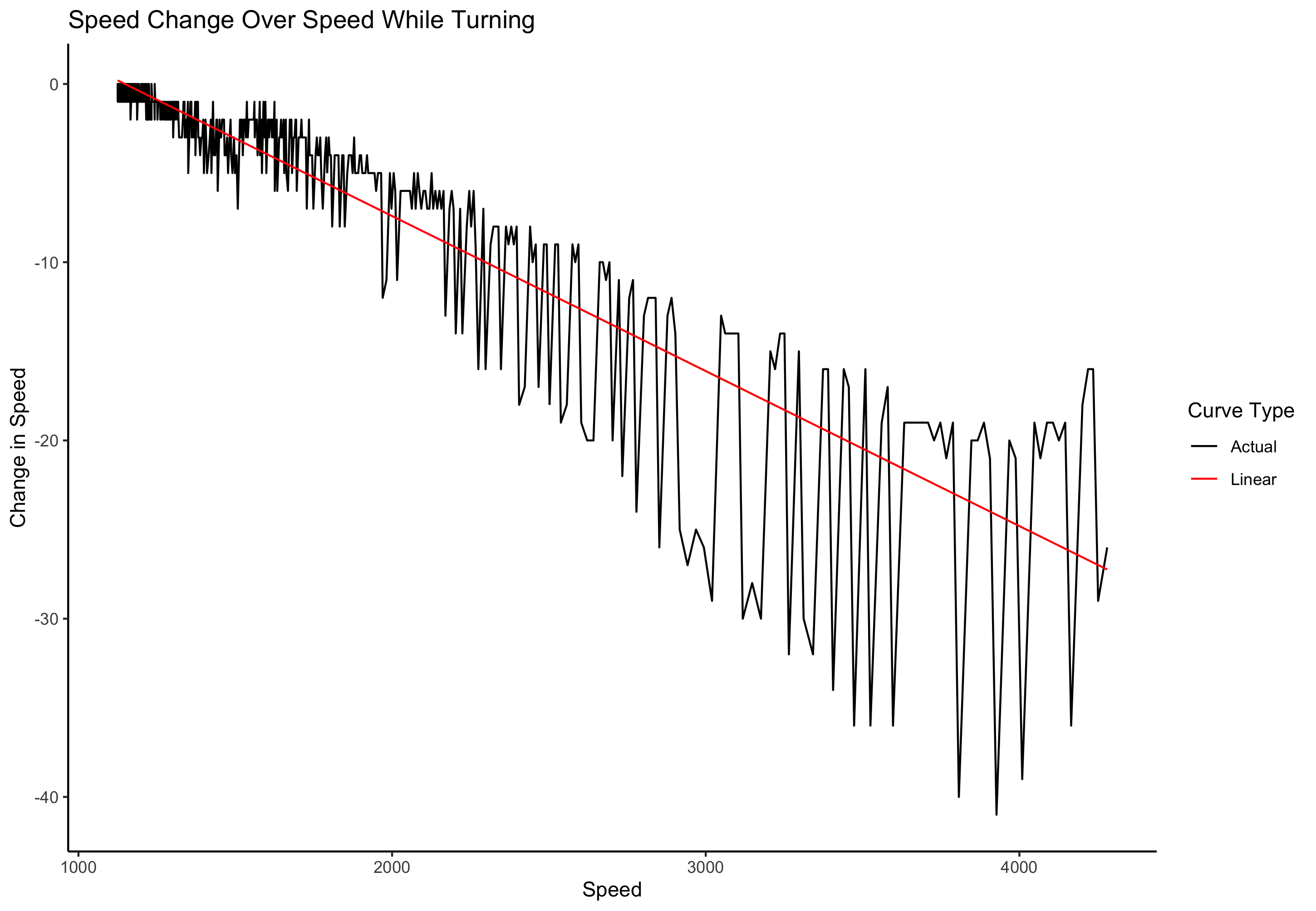
The fluctuations look dramatic on this graph because the y axis scale is so small. I double-checked the footage and am sure that I accurately recorded the changes in speed. I am not sure why fluctuations occur⁠—I suspect some oddness in the game’s flight model. At any rate, linear regression struck me as most sensible here.

That’s air friction accounted for. I also accounted for gravity. Though I could just as well have flown straight up/straight down at full throttle to measure the effect on speed, similar to my approach in measuring air friction, this seemed unnecessary. Unlike air friction, the effect of gravity on speed shouldn’t depend on how fast the player is going. Therefore, I estimated a constant value based on footage.

In summary, the steps toward calculating the player’s speed are:

    - Determine whether they are throttling up, braking, or idling, and solve for the next time step along the relevant curve, as mentioned. Scale the increase or decrease in speed by throttle/braking intensity.

    - If the player is turning, solve for the next time step along the turning curve to determine how strongly air friction should slow them down. Scale this decrease based on how sharply the player is turning.

    - Apply the gravitational constant, scaled by the player’s pitch (i.e., gravity has no effect when flying straight and maximum effect when angled straight up or down).

Stalling

I recorded the speed at which the first signs of stalling manifest (nose dipping, stall warning) in AC3, and then the speed at which a stall becomes so severe that the player loses control of the plane completely. In my flight model, if the player’s speed is between these two values, their control of the plane is reduced and the nose begins to dip, with severity depending on how close they are to the “hard limit” of about 150 speed.

Effect of Air Friction on Turn Rate

I account for the effect of air friction on turning speed in a similar way. I measured the fastest possible turning rate by timing a 360 degree flat turn in the game at the slowest speed I could, then measured the slowest possible turn rate by timing the same turn near max speed. Neither of these measurements were perfect, since speed is constantly reduced by air friction during the turn, but it was enough to roughly calculate air friction’s effect. The player’s pitch and yaw rate are scaled based on their speed; roll rate is also scaled, but to a lesser degree.

Angle of Attack

I tried two methods to implement angle of attack. The first was to take the average of the player’s rotations over the past 60 frames or so, then move them in that direction, rather than in the direction they are currently facing. In theory, this method is flawed because it weighs old frames as strongly as recent ones. The second method I tried was similar, but with a weighted average instead, such that more recent frames influenced the player’s travel direction more. In practice, both methods resulted in a similar-feeling effect.

Closing

That’s about it⁠—while the model is not perfectly accurate, I think it recreates the feel of AC3 using pretty simple and intuitive concepts and serves as a good base for game development. If I want to get more obsessive about replicating the AC3 flight model, I can always look into hacking/memory editing to do things like fix the player’s speed to a constant value while I measure turn rate, or I could even try to decompile the game. For now, though, I’d like to get on with making my own game. Thanks for reading.

←